B+ Tree Database in Modern C++
A B+ Tree based local database in Modern C++.
What is B+ Tree
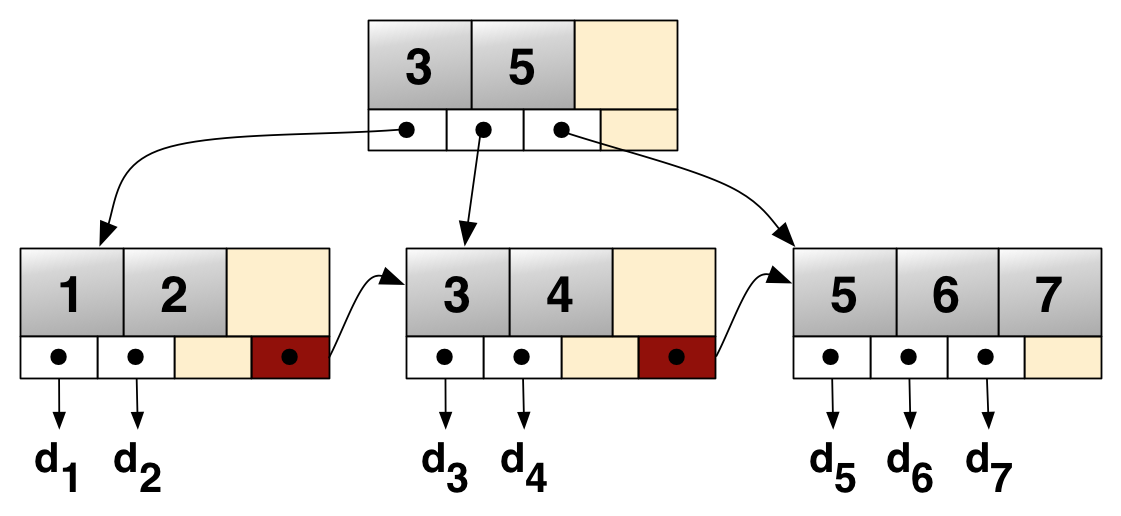
A B+ Tree is an m-ary tree with a variable but often large number of children per node. A B+ Tree often consists of a root, internal nodes and leaf nodes. It can be viewed as a variation of B-Tree in which each node contains only keys instead of key-value pairs, and to which an additional level is added at the buttom with linked leaves.
The primary value of a B+ tree is in storing data for efficient retrieval in a block-oriented filesystems. XFS, BFS, NSS, etc. all use B+ Tree for metadata indexing; BFS and NTFS also uses B+ Tree for storing directories.
Features of B+ Tree
-
Balanced: B+ Tree is self-balancing, which means that as the record is inserted or removed from the tree, it should be able to automatically adjust itself to rebalance its structure and keep the height low.
-
Multi-level: B+ Tree is multi-level structure, with a root node at the top and multiple levels of internal nodes below it. Only the leaf nodes at the bottom level contains the actual data.
-
Ordered: B+ Tree is ordered, which makes it easier to perform a search and other operations that require sorted data.
-
Fan-out: B+ Tree has a high fan-out, which means that each node contains many child nodes. This reduces the height of the tree.
Data Structure
To make it easier to manage the data, binary storage of records will be used and the database files will be stored under ./database with a .bin extension. Database operations will be disk-based, using a 50th order B+ Tree, a self-balancing multiplexed search tree to store the data.
Define a key_t to represent the key, initialized to the string char k[16], the keyCmp function is used to compare the size of the two key_t, overload the operators based on the keyCmp, and package them into a macro, for more convenient to compare:
1
2
#define OPERATOR_RELOAD (type)
#define KEYCMP_OPERATOR_RELOAD
Define a value_t to represent the value, which is char name[256], int value (the integer value entered by the user, which can be age, number, date, etc.) and char data[256].
In include/bplus.h, maintain a meta_t structure for storing metadata about the database, which will contain: order (number of orders), height, key_size, value_size, internal_num, leaf_num, root_offset, leaf_offset, slot (available slot offset).
Maintains an index_t structure for storing indexes, containing key and child.
Maintains an internal_t structure for storing internal nodes (all nodes except root and leaves) containing parent (parent offset), next (next internal node offset), prev, num (number of children), children[BPLUS_ORDER] (an array of children, of size is the tree order, used to store the index)
Maintains a leaf_t for storing leaf nodes, containing parent (parent offset), next (next node offset), prev, num (number of children), children[BPLUS_ORDER].
Maintains a record_t structure for storing records, containing key and value.
Create a B+ Tree
Initialization
-
Init the
meta -
Init root and leaf
-
unmap
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// bplus.cpp
void BPlusTree::initEmpty(){
// init meta
memset(&meta, 0, sizeof(meta_t));
meta.order = BPLUS_ORDER;
meta.value_size = sizeof(value_t);
meta.key_size = sizeof(key_t);
meta.height = 1;
meta.slot = OFFSET_BLOCK;
// init root node
internal_t root;
root.parent = 0;
root.prev = root.next = 0;
meta.root_offset = alloc(&root);
// init leaf
leaf_t leaf;
leaf.next = leaf.prev = 0;
leaf.parent = meta.root_offset;
root.children[0].child = alloc(&leaf);
meta.leaf_offset = root.children[0].child;
// unmap to disk
unmap(&meta, OFFSET_META);
unmap(&root, meta.root_offset);
unmap(&leaf, root.children[0].child);
}
Selection
- Time Complexity: O(logn)
- Space complexity: O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
// bplus.cpp
off_t BPlusTree::searchIndex(const key_t& key) const{
off_t index = meta.root_offset;
int height = meta.height;
while(height > 1){
internal_t node;
map(&node, index);
index_t *i = std::upper_bound(begin(node), end(node) - 1, key);
index = i -> child;
height--;
}
return index;
}
off_t BPlusTree::searchLeaf(off_t index, const key_t& key) const{
internal_t node;
map(&node, index);
index_t *i = std::upper_bound(begin(node), end(node) - 1, key);
return i -> child;
}
int BPlusTree::searchRange(key_t *left, const key_t& right, value_t *values, size_t max, bool *next) const{
if(left == NULL || right < *left){
return -1;
}
off_t off_left = searchLeaf(*left);
off_t off_right = searchLeaf(right);
off_t off = off_left;
size_t i = 0;
record_t *b_rec, *e_rec;
leaf_t leaf;
while(off != off_right && off != 0 && i < max){
map(&leaf, off);
if(off_left == off){
b_rec = find(leaf, *left);
}else{
b_rec = begin(leaf);
}
e_rec = leaf.children + leaf.num;
for(; b_rec != e_rec && i < max; b_rec++, i++){
values[i] = b_rec -> value;
}
off = leaf.next;
}
if(i < max){
map(&leaf, off_right);
b_rec = find(leaf, *left);
e_rec = std::upper_bound(begin(leaf), end(leaf), right);
for(; b_rec != e_rec && i < max; b_rec++, i++){
values[i] = b_rec -> value;
}
}
if(next != NULL){
if(i == max && b_rec != e_rec){
*next = true;
*left = b_rec -> key;
}else{
*next = false;
}
}
return i;
}
int BPlusTree::search(const key_t& key, value_t *value) const{
leaf_t leaf;
map(&leaf, searchLeaf(key));
record_t *record = find(leaf, key);
if(record != leaf.children + leaf.num){
*value = record -> value;
return keyCmp(record -> key, key);
}else{
return -1;
}
}
searchIndex is index traversal function, using the height get from meta establish the loop,map each index searched and with the help of std::upper_bound, find and return the top of the index (if not found, then return to the end of the sequence and enter the next loop )
searchLeaf is a leaf search function, the arguments are the index obtained from searchIndex and the target key to be selected,
Map the searched index to the node, again using std::upper_bound to find and return the child of the leaf node.
In order to simplify the call, overload the function:
1
2
3
4
// include/bplus.h
off_t searchLeaf(const key_t &key) const{
return searchLeaf(searchIndex(key), key);
}
In the function search, call searchLeaf(key) to find the leaf node where the key of the target record is located, and map to leaf, through the std::upper_bound to find the key, we need to judge whether the record searched is not the last, that is, successfully searched for the target record, then take the value of the record and assigned to the memory pointed to by the value passed into the function, the search returns the value of keyCmp(record → key, key). If the searched record is the last, that is, did not find the target record, then return -1 to error handling.
Insertion
- Time Complexity: O(logn)
- Space complexity: O(1)
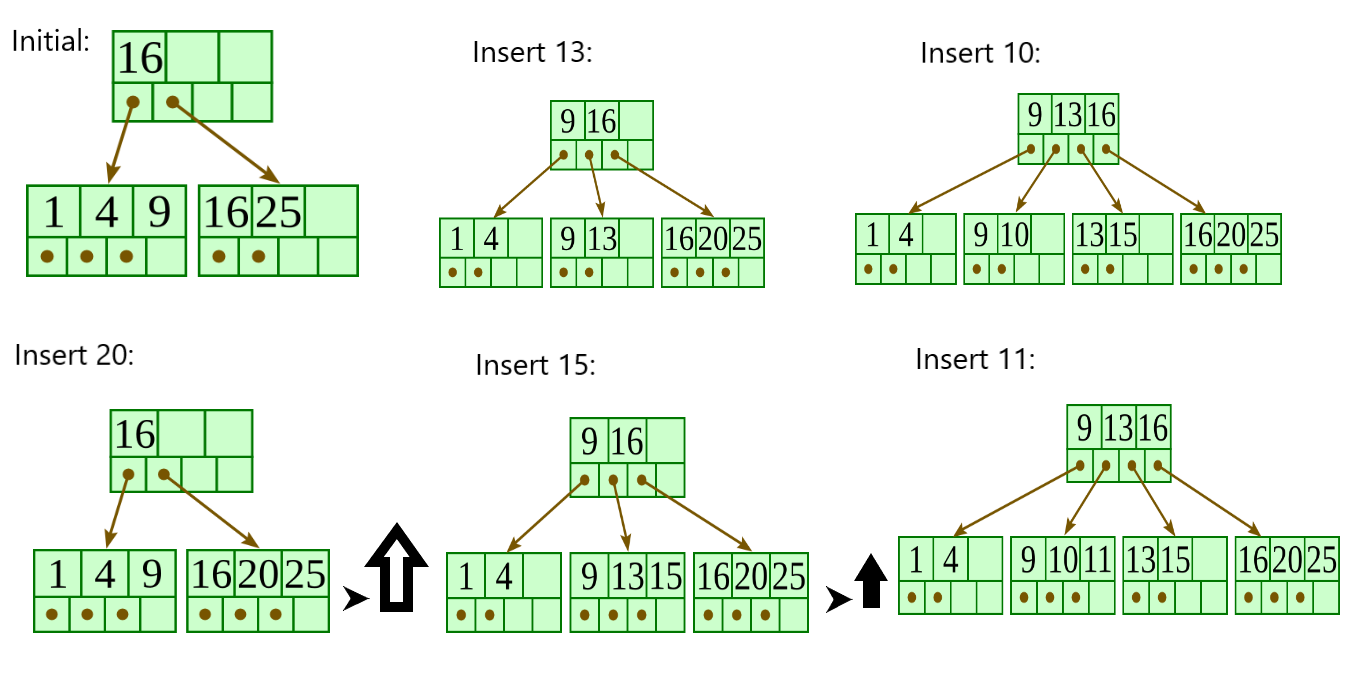
In a B+ Tree, every record is inserted into the bottom level. The insertion will be in increasing order only if there is no overflow.
If there is overflow in leaf node, we should split the node into two nodes, each node contains half of the tree’s order. First node contains ceil((order-1)/2) values.
If there is overflow in internal nodes, we should also split the node and first node contains ceil(m/2)-1 values.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
// bplus.cpp
void BPlusTree::insertRecNoSplit(leaf_t *leaf, const key_t& key, const value_t& value){
record_t *where = std::upper_bound(begin(*leaf), end(*leaf), key);
std::copy_backward(where, end(*leaf), end(*leaf) + 1);
where -> key = key;
where -> value = value;
leaf -> num++;
}
void BPlusTree::insertKeyNoSplit(internal_t& node, const key_t& key, off_t value){
index_t *where = std::upper_bound(begin(node), end(node) - 1, key);
std::copy_backward(where, end(node), end(node) + 1);
where -> key = key;
where -> child = (where + 1) -> child;
(where + 1) -> child = value;
node.num++;
}
void BPlusTree::insertKey(off_t offset, const key_t& key, off_t old, off_t after){
if(offset == 0){ // create root
internal_t root;
root.next = root.prev = root.parent = 0;
meta.root_offset = alloc(&root);
meta.height++;
root.num = 2;
root.children[0].key = key;
root.children[0].child = old;
root.children[1].child = after;
unmap(&meta, OFFSET_META);
unmap(&root, meta.root_offset);
resetParent(begin(root), end(root), meta.root_offset);
return;
}
internal_t node;
map(&node, offset);
if(node.num == meta.order){ // full split
// find split point
size_t point = (node.num - 1) / 2;
bool place_right = node.children[point].key < key;
if(place_right) point++;
if(place_right && key < node.children[point].key) point--;
key_t mid = node.children[point].key;
internal_t new_node;
createNode(offset, &node, &new_node);
// split
std::copy(begin(node) + point + 1, end(node), begin(new_node));
new_node.num = node.num - point - 1;
node.num = point + 1;
if(place_right){
insertKeyNoSplit(new_node, key, after);
}else{
insertKeyNoSplit(node, key, after);
}
unmap(&node, offset);
unmap(&new_node, node.next);
resetParent(begin(new_node), end(new_node), node.next);
insertKey(node.parent, mid, offset, node.next);
}else{
insertKeyNoSplit(node, key, after);
unmap(&node, offset);
}
}
int BPlusTree::insert(const key_t& key, value_t value){
off_t parent = searchIndex(key);
off_t offset = searchLeaf(parent, key);
leaf_t leaf;
map(&leaf, offset);
if(std::binary_search(begin(leaf), end(leaf), key))
return 1; //find same, return
if(leaf.num == meta.order){
// full, split
leaf_t new_leaf;
createNode(offset, &leaf, &new_leaf);
// find split point
size_t point = leaf.num / 2;
bool place_right = leaf.children[point].key < key;
if(place_right)
point++;
// split
std::copy(leaf.children + point, leaf.children + leaf.num, new_leaf.children);
new_leaf.num = leaf.num - point;
leaf.num = point;
if(place_right){
insertRecNoSplit(&new_leaf, key, value);
}else{
insertRecNoSplit(&leaf, key, value);
}
unmap(&leaf, offset);
unmap(&new_leaf, leaf.next);
insertKey(parent, new_leaf.children[0].key, offset, leaf.next);
}else{
insertRecNoSplit(&leaf, key, value);
unmap(&leaf, offset);
}
return 0;
}
insertRecNoSplit is used to handle record insertion operations that do not split nodes. This insertion operation searches for the insertion point where in the target leaf using std::upper_bound, performs an overwrite operation using std::copy_backward to shift the node after the insertion point backward to make room for the insertion of the record, and finally updates the number of children and the value, then finally update the number of leaf children.
insertKeyNoSplit is used to handle index insertion operation without splitting the node, this insertion operation will search for the index insertion point where in the internal node using std::upper_bound, use std::copy_backward to perform an overwrite operation to shift the index after the insertion point backward, to make room for the index, and finally refactor the index and update the children, the children pointed to by where should be changed to the children of (where + 1) (i.e., the original children pointed to by the index at that position), and the children of (where + 1) are the passed value argument (i.e., the original children pointed to by (where+1))
insertKey is used to handle key insertion operation, if the offset is 0, then create the root, if not, then insert operation, insert operation is divided into two kinds of insertion operation, one is directly without splitting insertion, that is, call insertKeyNoSplit and unmap to disk, the other when the number of nodes reaches the definition of the number of orders (meta.order), split: first find the split point, find the evenly split point (point), then create a new internal node (using the createNode), use std::copy to split and update the number of children, after splitting, and then call insertKeyNoSplit to insert the node (here, use the overloaded operator for the comparison of key_t), place_right==true insert the new node, and vice versa insert the old node), unmap to disk, and finally need to call resetParent and insertKey to adjust the parent node, to complete the insertion and the data structure rebalance operation.
insert is used to deal with the insertion of records, first through the search method to locate the insertion point and the parent offset. Map offset to leaf, a run binary_search, if the same record is found, return -1, otherwise perform the insertion operation. Insertion operation is divided into two cases, if the number of records does not reach the order, that is, do not need to split, insert with the insertRecNoSplit and unmap to disk; if the number of records to reach the order, need to split: createNode to create a new node, simple calculation to get the point, determine whether place_right, finally, start splitting. Use std::copy to split and update the children information, and insertRecNoSplit to insert and unmap to disk. Eventually, insertKey is used to insert the new leaf into the parent, further updating the parents to maintain a balanced structure.
Deletion
- Time Complexity: O(logn)
- Space complexity: O(1)
Deleting an element on a B+ tree consists of three main events: searching the node, deleting the key and balancing the tree if required.
Underflow is a situation when there is less number of keys in a node than the minimum number of keys it should hold.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
// bplus.cpp
void BPlusTree::removeNode(T *prev, T *node){
unalloc(node, prev -> next);
prev -> next = node -> next;
if(node -> next != 0){
T next;
map(&next, node -> next, SIZE_NO_CHILDREN);
next.prev = node -> prev;
unmap(&next, node -> next, SIZE_NO_CHILDREN);
}
unmap(&meta, OFFSET_META);
}
void BPlusTree::removeIndex(off_t offset, internal_t& node, const key_t& key)
{
size_t min = meta.root_offset == offset ? 1 : meta.order / 2;
key_t index_key = begin(node) -> key;
index_t *to_delete = find(node, key);
if(to_delete != end(node)){
(to_delete + 1) -> child = to_delete -> child;
std::copy(to_delete + 1, end(node), to_delete);
}
node.num--;
if(node.num == 1 && meta.root_offset == offset && meta.internal_num != 1){
unalloc(&node, meta.root_offset);
meta.height--;
meta.root_offset = node.children[0].child;
unmap(&meta, OFFSET_META);
return;
} // delete root, decrease height, reset root
if(node.num < min){
internal_t parent;
map(&parent, node.parent);
bool borrowed = false;
if(offset != begin(parent) -> child)
borrowed = borrowKey(false, node, offset);
if(!borrowed && offset != (end(parent) - 1) -> child)
borrowed = borrowKey(true, node, offset);
if(!borrowed){
if(offset == (end(parent) - 1)->child){
internal_t prev;
map(&prev, node.prev);
index_t *where = find(parent, begin(prev) -> key);
resetParent(begin(node), end(node), node.prev);
mergeKey(where, prev, node);
unmap(&prev, node.prev);
}else{
internal_t next;
map(&next, node.next);
index_t *where = find(parent, index_key);
resetParent(begin(next), end(next), offset);
mergeKey(where, node, next);
unmap(&node, offset);
}
removeIndex(node.parent, parent, index_key);
}else{
unmap(&node, offset);
}
}else{
unmap(&node, offset);
}
}
int BPlusTree::remove(const key_t& key){
internal_t parent;
leaf_t leaf;
off_t parent_off = searchIndex(key);
map(&parent, parent_off);
index_t *where = find(parent, key);
off_t offset = where -> child;
map(&leaf, offset);
if(!std::binary_search(begin(leaf), end(leaf), key))
return -1; // cannot find
size_t min = meta.leaf_num == 1 ? 0 : meta.order / 2;
record_t *to_delete = find(leaf, key);
std::copy(to_delete + 1, end(leaf), to_delete);
leaf.num--;
if(leaf.num < min){
bool borrowed = false;
if(leaf.prev != 0)
borrowed = borrowKey(false, leaf);
if(!borrowed && leaf.next != 0)
borrowed = borrowKey(true, leaf);
if(!borrowed){
key_t index_key;
if(where == end(parent) - 1){
leaf_t prev;
map(&prev, leaf.prev);
index_key = begin(prev)->key;
mergeLeaf(&prev, &leaf);
removeNode(&prev, &leaf);
unmap(&prev, leaf.prev);
}else{
leaf_t next;
map(&next, leaf.next);
index_key = begin(leaf)->key;
mergeLeaf(&leaf, &next);
removeNode(&leaf, &next);
unmap(&leaf, offset);
}
removeIndex(parent_off, parent, index_key);
}else{
unmap(&leaf, offset);
}
} else {
unmap(&leaf, offset);
}
return 0;
}
removeNode is simple, unalloc the node (update the meta), transfer the successor of the deleted node to the predecessor, if the deleted node is not the last node, map the successor of the node, transfer the predecessor of the node to its predecessor and unmap it to disk, and finally unmap the meta, the whole operation is actually a linear table operation.
removeIndex is used to remove the index, min is used as the minimum number of nodes, if it is not the root, min is half of the order. to_delete is the index for deletion, use find to locate it, if to_delete is not the last index, transfer his children to the latter index and overwrite it with std::copy, if to_delete is the root and there is only one node, then delete it directly and update root_offset to reduce the tree height to balance the tree structure. If the number of children of the node where to_delete is located is less than min, it is necessary to borrow and merge. Record the father parent, the state of whether borrowed (a boolean), if the offset is the first child of the father, borrow from the left node, and vice versa from the right node, borrowing node are implemented using borrowKey, which uses two sets of overloading to deal with leaf and internal nodes, for leaf: lender_off through the incoming boolean value from_right to determine the lender offset, with the help of this offset map it to the lender, if the lender’s children did not reach the half of the order, merge the beginning of the lender to the end of the borrower, or merge the end of the lender to the beginning of the borrower, use changeParent to change the parent after splicing data with std::copy_backward, update the children, and finally applied to disk; for internal node is much the same, just one more step, change the node pointing. After completing the borrow operation, map the node’s predecessor or successor to prev/next, use mergeKey to merge the keys, in mergeKey, use std::copy to splice the left and right, update the children, and use removeNode to remove nodes that are discarded after the merge.
remove performs delete operation, use searchIndex and find to get and map parent with leaf, return -1 if the key is not found in leaf (use binary_search), determine the minimum number of nodes min, with delete point to_delete, use std::copy to override, if the number of leaf is less than the minimum number of nodes, set borrowed to indicate the state of borrowing. We need to set three judgments, if the leaf precursor is not 0, borrow from the left, if the successor is not 0, borrow from the right, after the borrowing and lending of left/right, it is still unborrowed state, the leaf precursor will be mapped to prev. Record the key, merge the leaf and the precursor into one node, delete the leaf, complete the right-merge operation. Otherwise perform the left-merge operation, after the merge operation, of course, unmap to disk. Completion of leaf deletion, need to delete in the index, call removeIndex(parent_off, parent, index_key) to realize the deletion.
Update
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// bplus.cpp
int BPlusTree::update(const key_t& key, value_t value){
off_t offset = searchLeaf(key);
leaf_t leaf;
map(&leaf, offset);
record_t *record = find(leaf, key);
if(record != leaf.children + leaf.num){
if(key == record -> key){
record->value = value;
unmap(&leaf, offset);
return 0;
}else{
return 1;
}
}else{
return -1; // not found
}
}
The update algorithm is implemented using update(const key_t& key, value_t value), using searchLeaf to find the target offset and map it, if not found then return -1, otherwise determine whether the found record key matches the provided one, (because the essence of find is implemented as std::lower_bound. find the key may be the first key greater than the target rather than the one we need to be exactly equal to the target, so a futher judgment is necessary), match then update the value of the record, umap and return 0, does not match then return 1 error.
- Time Complexity: O(logn)
- Space complexity: O(1)
Interface
For better management, design a shell-like user interface. Define to handler for commands handling.
1
2
3
// main.cpp
using CommandHandler = void(*)(const string& arg);
using OptionHandler = void(*)(const string& arg);
Use two map and lambda funtion to store correspondence of commands and handlers.
1
2
3
// main.cpp
map<string, OptionHandler> optionMap = {........};
map<string, CommandHandler> commandMap = {........};
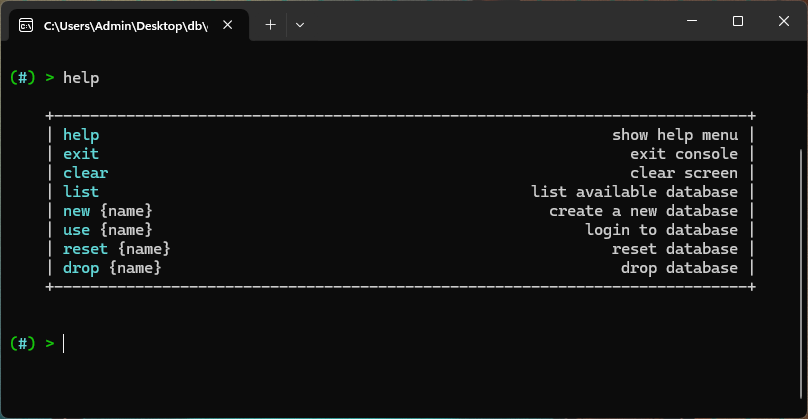
After launching the program, it will firstly enter the optionLoop for database management:
1
2
3
4
5
6
7
8
help show help menu
exit exit console
clear clear screen
list list available database
new {name} create a new database
use {name} login to database
reset {name} reset database
drop {name} drop database
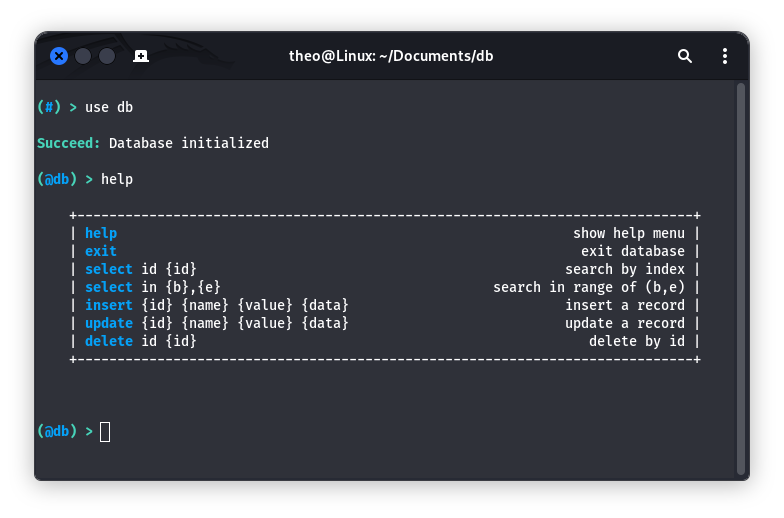
Use use command to login the database and enter the second commandLoop for data management:
1
2
3
4
5
6
7
help show help menu
exit exit database
select id {id} search by index
select in {b},{e} search in range of (b,e)
insert {id} {name} {value} {data} insert a record
update {id} {name} {value} {data} update a record
delete id {id} delete by id
Compile and Test
Platform:
-
Linux 6.11.2-amd64 #1 SMP PREEMPT_DYNAMIC x86_64 GNU/Linux
-
gcc version 14.2.0 (Debian 14.2.0-8)
Make and Run
We could have a Makefile to compile the whole source:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
CXX = g++
SRC_DIR = ./
TARGET = easydb
OBJ = main.o bplus.o
$(TARGET):$(OBJ)
$(CXX) -o $(TARGET) $(OBJ)
rm -rf $(OBJ)
main.o:
$(CXX) -c $(SRC_DIR)main.cpp
bplus.o:
$(CXX) -c $(SRC_DIR)bplus.cpp
clean:
rm -rf $(OBJ) $(TARGET)
CMake is another option easy to use:
1
2
3
4
5
6
7
8
9
10
cmake_minimum_required(VERSION 3.10)
project(easydb)
add_executable(easydb main.cpp bplus.cpp)
include_directories(${PROJECT_SOURCE_DIR}/include)
add_compile_options(-fexec-charset=UTF-8)
add_compile_options(-finput-charset=GBK)
add_compile_options(-fwide-exec-charset=UTF-8)
To build the program, just simply use make. The target output will be ./easydb.
Build on Windows
On Windows, we should first setup the Mingw64. For example, we could use w64devkit-x64. Don’t forget to set the environment variable PATH to the path of w64devkit-x64’s bin folder.
After successfully installing Mingw64, use cmake-gui to configure and generate the Makefile and then use make to compile the program. This will generate a executable file named easydb.exe.
Test Insertion
C++
We can write a simple test script with shell or python to test the program, here’s an example in C++ running on Linux:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
// test.cpp
#include <iostream>
#include <fstream>
#include <thread>
#include <chrono>
#include <sys/types.h>
#include <sys/stat.h>
#include <fcntl.h>
#include <unistd.h>
int main(){
const int num_inserts = 100000;
const char* pipe_name = "pipe";
mkfifo(pipe_name,0666);
std::ofstream logFile("time.log");
std::streambuf *coutbuf = std::cout.rdbuf();
std::cout.rdbuf(logFile.rdbuf());
std::thread easydb_thread([pipe_name]() {
std::system("./easydb < pipe &");
});
int fd = open(pipe_name, O_WRONLY);
auto start_time = std::chrono::high_resolution_clock::now();
auto start_duration = start_time.time_since_epoch();
auto milliseconds = std::chrono::duration_cast<std::chrono::milliseconds>(start_duration).count();
std::cout << "[" << milliseconds << "]: ";
std::cout << "Start insert test" << std::endl;
std::string command;
command = "use db\n";
write(fd, command.c_str(), command.length());
std::this_thread::sleep_for(std::chrono::seconds(2));
for (int i = 1; i <= num_inserts; ++i) {
command = "insert " + std::to_string(i) + " name" + std::to_string(i) + " " + std::to_string(i) + " item" + std::to_string(i) + "@data\n";
write(fd, command.c_str(), command.length());
}
command = "exit\n";
write(fd, command.c_str(), command.length());
command = "exit\n";
write(fd, command.c_str(), command.length());
auto end_time = std::chrono::high_resolution_clock::now();
auto elapsed_time = std::chrono::duration_cast<std::chrono::seconds>(end_time - start_time);
auto stop_duration = end_time.time_since_epoch();
milliseconds = std::chrono::duration_cast<std::chrono::milliseconds>(stop_duration).count();
std::cout << "[" << milliseconds << "]: ";
std::cout << "Insert " << num_inserts << " records, time: " << elapsed_time.count() << " s" << std::endl;
close(fd);
easydb_thread.join();
unlink(pipe_name);
std::cout.rdbuf(coutbuf);
return 0;
}
The test program will open a pipe then insert 100000 records to the database db, it records the duration time and write to the log time.log. Build the test program with g++:
1
$ g++ test_insert.cpp -o test
In the log file time.log, for example:
1
2
[timexxxxxxxxxx]: Start insert test
[timexxxxxxxxxx]: Insert 100000 records, time: 4 s
Shell
A simple Shell script as an example:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#!/bin/bash
easydb_path="./easydb"
num_inserts=10000
mkfifo pipe
$easydb_path < pipe &
start_time=$(date +%s)
echo "use db" >> pipe
for i in $(seq 1 $num_inserts); do
echo "insert $i name$i $i item$i@data" >> pipe
done
echo "exit" >> pipe
echo "exit" >> pipe
wait
end_time=$(date +%s)
elapsed_time=$((end_time - start_time))
echo "Insert 100000 records, time: $elapsed_time s"
exec 9>&-
rm pipe
Python
A simple Python script as an example:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import subprocess
import time
import os
easydb_path = "./easydb"
num_inserts = 10000
os.mkfifo("pipe")
easydb_process = subprocess.Popen([easydb_path], stdin=open("pipe", "w"))
start_time = time.time()
with open("pipe", "w") as f:
f.write("use db\n")
for i in range(1, num_inserts + 1):
f.write(f"insert {i} name{i} {i} item{i}@data\n")
f.write("exit\n")
f.write("exit\n")
easydb_process.wait()
end_time = time.time()
elapsed_time = end_time - start_time
print(f"Insert {num_inserts} records, time: {elapsed_time:.2f} s")
os.unlink("pipe")
Source Code
Github: https://github.com/the0cp/db